Conjecturas sobre o desenvolvimento do raciocínio lógico

Passeando pelo Instagram, cheguei a um meme de um professor passando uma “prova” para sua classe do oitavo ano.

A ”prova” dizia o seguinte:

1. (10%) Resolva as equações:

   a) $2 + x = 4$

   b) $9 - y = 5$

2. (90%) De acordo com os valores do Ex. 1, determine o valor de $a$:

   $$a = (log_y x)^{-1} + 4 \det{(A^t)} - \arcsin{(x-1)}$$

   Onde $$A = \begin{bmatrix} x & 4 & y \newline \pi & 0 & 9 \newline -2 & 3 & 1 \newline \end{bmatrix}$$

Reprodução: Instagram/profahideki

E obviamente, todos comentários são sobre o exagero da “dificuldade” da prova.

Bom, pelo menos para o item 1, as soluções são muito simples: $x = 2$ e $y = 4$.

Perceba que, com os valores do primeiro item, a conta assustadora do item 2 se torna fácil. Até o temido arco-seno vira um cálculo trivial. O logaritmo é simplório. Apesar da resposta não fazer sentido nenhum numericamente – um ângulo somado a um número?

Obviamente é tudo um meme, e talvez a maioria das pessoas conseguiriam responder a questão. Mas é interessante pensar no que causa o medo, o susto, a ansiedade das pessoas em relação a algo que é meramente linear.

Conjecturando possibilidades, talvez existam duas habilidades principais e talvez negligenciadas no desenvolvimento das crianças: A capacidade de dividir problemas grandes em problemas menores e a capacidade de planejar a execução de soluções.

Reduzindo a problemas menores

Não me lembro muitas vezes na escola de ver problemas que envolvessem, por exemplo, equações quadráticas e matrizes ao mesmo tempo.

Acho que talvez a maioria das pessoas nunca pensaram em problemas do tipo. Nunca viram algo assim. E isso não significa que não exista. Mas é desenvolvido um pensamento unário sobre a classe dos problemas. Um problema só pode pertencer a um conjunto específico de métodos de resolução.

Essa falta de conectar a matemática, e digo isso pensando em conectar tópicos diferentes da disciplina com outros diferentes, crie um comportamento nas crianças de que os problemas não têm conexão; de que o conjunto dos problemas de equações quadráticas é diferente do conjunto de problemas de logaritmos ou matrizes por exemplo.

Na verdade, tudo faz parte do mesmo conjunto: a matemática em si.

A gente vê isso desde pequeno mesmo, quando os colegas de classe as vezes perguntavam: “Esse problema é de multiplicação ou de soma, ou de divisão?”. Essas operações fazem parte de um mesmo conjunto de ferramentas matemáticas e muitas vezes se combinam para resolver um problema. E as vezes a pergunta “Mas eu posso somar tal X com tal Y?”, demonstrando a falta de de fato compreender a função das técnicas da matemática.

O ponto que quero chegar aqui é que se aprende a olhar para os problemas como aplicações de uma técnica exclusiva. De que só é possível resolver coisas se conhecer o passo-a-passo. É um pensamento de que só é possível solucionar problemas por meio de um conjunto de regras que permite deduzir sobre o quê é um determinado problema.

Isso é essencialmente olhar para aquela equação grande como um único problema. Mas na verdade, é claro que são pequenos problemas menores. Primeiro você têm o problema de ter os valores de $x$ e $y$; por segundo, para achar o determinante da matriz, eu preciso ter a matriz – e lá embaixo está ela, definida.

Mas perceba também que isso exigiu alguma habilidade minha de planejar o quê fazer. Ao olhar o problema eu primeiro deveria me preocupar se terá uma maneira de resolver ele. Acho que como disse, o primeiro olhar que ensinamos as crianças é olhar para problemas e tentar identificar técnicas e não planejamentos com os pedaços de conhecimentos que temos.

Capacidade de planejamento mental

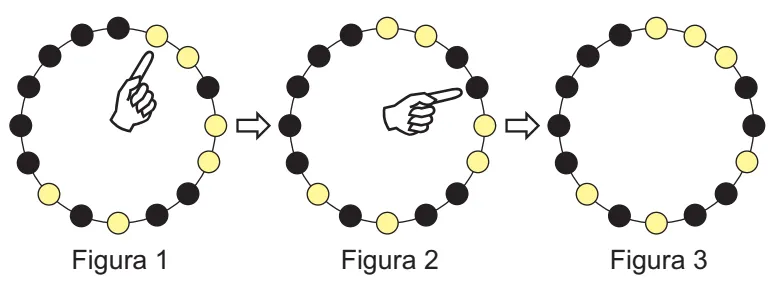
Eu vou colocar aqui um dos problemas de matemáticas mais legais que eu já vi. É da OBMEP, Olimpíada Brasileira de Matemáticas da Escolas Públicas e Privadas. Nível 2, de 2017.

Dezesseis botões pretos ou amarelos estão igualmente dispostos num círculo. Toda vez que apertamos um botão, seus dois vizinhos, e somente eles, mudam de cor. No exemplo ao lado, vemos o que acontece quando apertamos o botão amarelo indicado na Figura 1 e, depois, o botão preto indicado na Figura 2.

Reprodução: OBMEP, 2017, Nível 2.

E a pergunta do item do C:

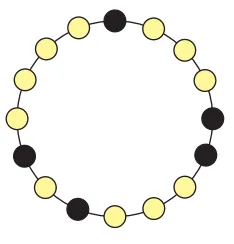
Explique por que, a partir da figura abaixo, é impossível apertar botões de forma que todos fiquem amarelos ao mesmo tempo.

Antes do item C, tem o item B, que nos guia até a possível solução:

A partir de uma figura com 10 botões pretos e 6 amarelos, explique por que, independentemente de quantos e quais forem os botões apertados, o número de botões pretos sempre será par.

Veja que este é um problema com uma solução muito simples – envolve explicar que no item C, sempre haverá um número ímpar de lâmpadas acesas (tente explicar), enquanto o círculo tem um número par de lâmpadas.

Mesmo com a dica para pensar em paridade, a verdade é que a que a maioria das pessoas no Brasil não conseguem acompanhar um raciocínio linear. Elas não percebem que o item C, na verdade é uma continuação do item B.

Tragicamente, é preciso que alguém tenha ensinado esse problema bem específico para elas. Falta pensar que de um problema anterior, eu consiga facilitar resolver um problema posterior.

Então agora imagine que voltamos aquela prova do início desse texto. Eu imagino que a maioria das crianças conseguiria resolver partes da questão maior se você dividisse ela em partes menores: primeiro calcular o determinante, segundo o logaritmo, etc.

Mas, tristemente, se mesmo depois disso você colocasse a equação inteira, é provável que grande parte não conseguiria perceber o planejamento da resolução: como nas questões anteriores elas estavam resolvendo pequenas partes do problema maior.

Essa é a falha no desenvolvimento de uma habilidade que permita olhar para um problema e pensar: “o quê eu já sei? E o quê eu ainda não sei? E como eu posso descobrir isso? E para onde isso vai me levar? Mais perto ou mais longe da resposta? E o quê fazer depois?”.

Note como isso é tão parecido quanto quebrar problemas grandes em problemas menores.

Parece que falhamos em exercitar as crianças a visualizarem caminhos lineares, mesmo que simples, e quê tudo se resume ao clássico: “Como que resolve esse problema?” e um guia passo-a-passo.

Extrapolando para adultos

Meus exemplos foram baseados empiricamente com o que notei durante minha infância, estudando em uma escola mediana do estado de São Paulo. Mas na realidade, essa talvez seja a dificuldade da maioria das pessoas.

Trabalhando como engenheiro de software, o dia-a-dia é basicamente isso. Planejar e dividir em sub-problemas. É uma habilidade singela, mas a verdade é que a maioria dos adultos tiveram falhas em seu desenvolvimento escolar que não permitiram elas entenderem que qualquer indivíduo, a partir de conclusões menores, consegue construir soluções maiores. Que na verdade, você não precisa saber construir uma casa em si, mas sim saber fazer a fundação, as paredes, o telhado… Que as coisas são um quebra-cabeça conectado.

Para a maioria das pessoas que tiveram uma educação adequada, isso é banal, mas eu conjecturo que infelizmente, essa linha de pensamento essencial, é algo não perceptível para a maioria das pessoas, especialmente no Brasil.

Se exercitamos nas crianças as ideias de desmontar problemas e planejar soluções, estaremos dando a elas uma ferramenta essencial para a vida — não só para a matemática, mas para qualquer desafio que encontrarem pelo caminho.

Mas não sei… São apenas conjecturas de como surgem as falhas e incapacidade de pensamento lógico em nosso sistema de educação. E como algo tão banal, é combustível de uma desigualdade de oportunidades e produtividade.